Chapter 10 Moderating, Mediating, and Confounding Variables
10.1 More than the IV and the DV
In this section, we’ll expand our understanding of variables in the study. So far, we have discussed three types of variables:
Independent variable (IV): The variable that is implied (quasi-experiment, non-experiment) or demonstrated to be (experiment) the cause of an effect. When there is a manipulation, the variable that is manipulated is the IV.
Dependent variable (DV): The variable that is implied or demonstrated to be the outcome.
Confounding variable: Also called a nuisance variable or third variable. This is a third variable that causes a change in both the IV and the DV at the same time. To borrow an example, we might observe a correlation between ice cream consumption and snake bites. We might wonder if eating ice cream causes snake bites on the basis of this result. Although this seems ridiculous, it’s easier for us to make these sorts of conclusions when the variables are psychological constructs (for example, personality and job outcomes). In this example, the weather is a confounding variable. When the weather is warmer, ice cream consumption (it’s warm) and snake bites (people go on hikes) increase.
From this example, you might wonder if other factors matter, such as the location (regions with lots of snakes versus regions with fewer). Some of these other variables may affect the DV in other ways, such as by weakening the relationship between the IV and the DV. Therefore, confounding variables are one type of extraneous variable. Extraneous variables include anything we have not included in our study.
Some extraneous variables are not likely to affect anything. In this example, the gender of people buying ice cream probably does not affect their likelihood of snake bites. Other extraneous variables can affect the relationship we are trying to observe in our study. Whenever you design a study, an important step is to stop and consider “what else could be affecting this relationship?” When you do this, you will brainstorm a list of possible confounding and extraneous variables. Then, you’ll decide if the variables are likely to affect the relationship of interest. If they are, then usually you can redesign your study to avoid them.
To summarize: A study is essentially a search to identify and explain relationships between IVs and DVs. When claims about the relationship between an IV and DV are true, the claim has internal validity.
Next, we will explore two more complex relationships between variables that develop when we add a second IV to our model.
10.2 Moderating Variables: Interaction Effects
Interactions are also called moderated relationships or moderation. An interaction occurs when the effect of one variable depends on the value of another variable. ** For example, how do you increase the sweetness of coffee? Imagine that sweetness is the DV, and the two variables are stirring (yes vs no) and adding a sugar cube (yes vs no).
We diagram a moderated relationship using this notation:
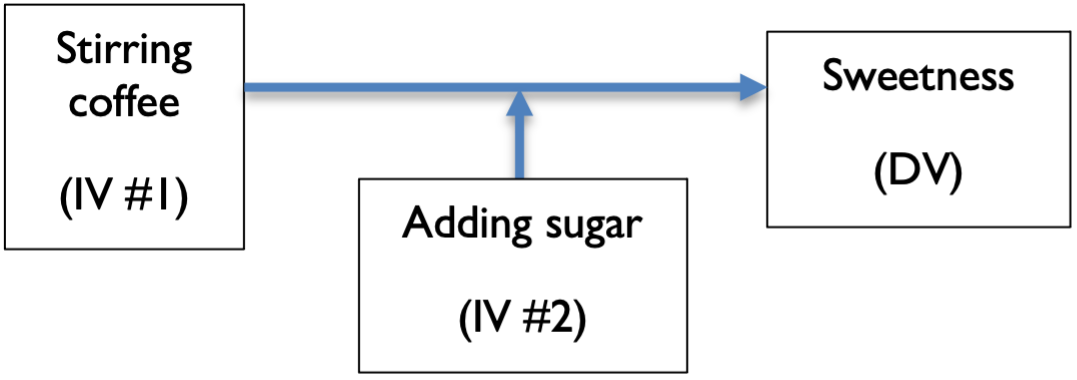
Diagram of a moderated relationship with IV 2 and IV 1 interacting to affect DV
And, when we have group means for every condition, we can see the impact of these two factors (factor is a fancy word for IV) in a table:
| . | Stirring: Yes | Stirring: No |
|---|---|---|
| Sugar: Yes | \(\bar{X}_{sweet}=100\) | \(\bar{X}_{sweet} = 0\) |
| Sugar: No | \(\bar{X}_{sweet}=0\) | \(\bar{X}_{sweet} = 0\) |
When is the coffee sweet? Stirring alone does not change the taste of the coffee. Adding a sugar cube alone also doesn’t change the taste of the coffee, since the sugar will just sink to the bottom. It’s only when sugar is added, and the coffee is stirred that it tastes sweet.
We can say there is an interaction between adding sugar and stirring coffee. The effect of the stirring depends on the value of another variable (whether or not sugar is added).
10.3 Some Terminology
When more than one IV is included in a model, we are using a factorial design. Factorial designs include 2 or more factors (or IVs) with 2 or more levels each. In the coffee example, our design has two factors (stirring and adding sugar), each with two levels.
In factorial designs (i.e., studies that manipulate two or more factors), participants are observed at each level of each factor. Because every possible combination of each IV is included, the effects of each factor alone can be observed. We also get to see how these factors impact each other. We say this design is fully crossed because every possible combination of levels is included.
10.4 Main Effects
A main effect is the effect of one factor. There is one potential main effect for each factor.
In this example, the potential main effects are stirring and adding sugar. To find the main effects, find the mean of each column (i.e., add the two numbers and divide by 2). If there are differences in these means, there is a significant main effect for one of the factors. Next, find the mean of each row (add going across and divide by 2). If there are differences in these row means, then there is a main effect for the other factor.
| . | Stirring: Yes | Stirring: No | Row mean |
|---|---|---|---|
| Sugar: Yes | \(\bar{X}_{sweet}=100\) | \(\bar{X}_{sweet} = 0\) | \(\bar{X}_{sugar}= 50\) |
| Sugar: No | \(\bar{X}_{sweet}=0\) | \(\bar{X}_{sweet} = 0\) | \(\bar{X}_{\text{no sugar}}=0\) |
| Column mean | \(\bar{X}_{stir}=50\) | \(\bar{X}_{nostir}=0\) . |
In our example, we see two main effects. Adding a sugar cube (mean of 50) differs from not adding sugar (mean of 0). That’s the first main effect. The second is stirring; stirring (mean of 50) differs from not stirring (mean of 0).
10.5 Simple Effects
When an interaction effect is present, each part of an interaction is called a simple effect. To examine the simple effects, compare each cell to every other cell in the same row. Next, compare each cell to ever other cell in the same column. Simple effects are never diagonal from each other.
In our example, we see a simple effect as we go from Stir+Sugar to NoStir+Sugar. There is no simple effect between Stir+NoSugar and NoStir+NoSugar (both are 0). What makes this an interaction effect is that these two simple effects are different from one another.
On the vertical, there is a simple effect from Stir+Sugar to Stir+NoSugar. There is no simple effect from NoStir+Sugar to NoStir+NoSugar (both are 0). Again, this is an interaction effect because these two simple effects are different.
10.6 Interaction Effect
When there is at least one (significant) simple effect that differs across levels of one of the IVs (as demonstrated above), then you can say there is an interaction between the two factors. In a two-way ANOVA, there is one possible interaction effect. We sometimes show this with a multiplication symbol: Sugar*Stir. In our example, there is an interaction between sugar and stirring.
In summary: An interaction effect is when the impact of one variable depends on the level of another variable.
Interaction effects are important in psychology because they let us explain the circumstances under which an effect occurs. Anytime we say that an effect depends on something else, we are describing an interaction effect.
10.7 Mediators and Mediated Relationships
A mediated relationship is a chain reaction; one variable causes another variable (the mediator), which then causes the DV. Please forgive another silly example; I am including it to keep the example as simple as possible. Here is how we diagram it:

Diagram of a moderated relationship with IV 2 and IV 1 interacting to affect DV
This is a totally different situation that the previous one. The first variable is a preference for sweetness; do you like sweet foods and beverages? If participants prefer sweetness, then they will add more sugar. If they don’t prefer sugar in their coffee, then they will add less (or no) sugar. Thus, preference for sweetness is an IV that causes a change in the mediator, adding sugar. Finally, adding sugar is what causes the coffee to taste sweet. Any time we can string together three variables in a causal chain, we are describing a mediated relationship.
In summary: A mediated relationship occurs when one variable affects another (the mediator), and that variable (the mediator), affects something else.
Mediated relationships are important in psychology because they let us explain why or how an effect happens. The mediator is the how or the why. Why do participants who prefer sweetness end up with sweeter coffee? It is because they added sugar.